Section (category theory)

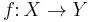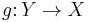In category theory, a branch of mathematics, a section (or coretraction) is a right inverse of a morphism. Dually, a retraction (or retract) is a left inverse. In other words, if $f\colon X\to Y$ and $g\colon Y\to X$ are morphisms whose composition 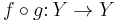$f\circ g\colon Y\to Y$ is the identity morphism on $Y$ , then $g$ is a section of $f$ , and $f$ is a retraction of $g$ .

If section of a morphism exists, it is called sectionable. Dually, if retraction of a morphism exists, it is called retractable.

The categorical concept of a section is important in homological algebra, and is also closely related to the notion of a section of a fiber bundle in topology: in the latter case, a section of a fiber bundle is a section of the bundle projection map of the fiber bundle.

Every section is a monomorphism, and every retraction is an epimorphism; they are called respectively a split monomorphism and a split epimorphism (the inverse is the splitting).

Examples

Given a quotient space 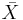$\bar X$ with quotient map 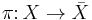$\pi\colon X \to \bar X$ , a section of $\pi$ is called a transversal.

Section (category theory)

Examples

See also